二次函数的压轴题类型有很多:二次函数图像综合考察、二次函数背景最值问题、二次函数与特殊图形、二次函数与面积等等,在那么多的类型里面,今天小编和大家分享在考试中出现机率较高的——二次函数与面积问题!传授一种一般学校老师不会教的暴强技巧!
求“半天吊”三角形面积暴强技巧:
如图1,过△ABC的三个顶点分别作出与水平垂直的三条线,外侧两条直线之间的距离叫△ABC的“水平宽”,中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”。三角形面积的新方法:,即三角形面积等于水平宽与铅垂高乘积的一半。
注意事项:
1.找出B、C的坐标,横坐标大减小,即可求出水平宽;
2.求出直线BC的解析式,A与D的横坐标相同,A与D的纵坐标大减小,即可求出铅垂高;
3.根据公式:S△=×水平宽×铅锤高,可求出面积。
真题分析:
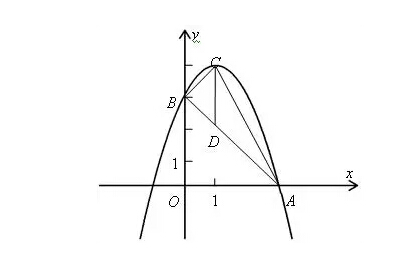
如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及;
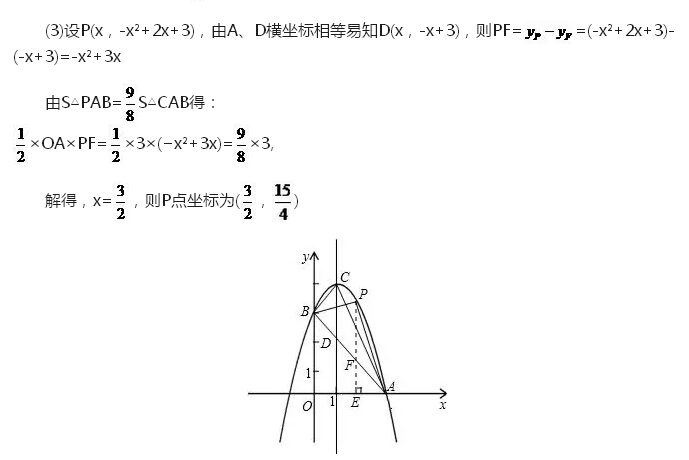
(3)在(2)中是否存在一点P,使,若存在,求出P点的坐标;若不存在,请说明理由.
解析:
(1)由顶点C(1,4),A(3,0)可以得出抛物线的解析式为:y1=-x2+2x+3,已知B点的坐标为(0,3),所以直线AB的解析式为:y2=-x+3
求函数解析式就是代点解方程(组)
(2)因为C点坐标为(1,4),把x=1代入y2=-x+3可得D(1,2),因此CD=4-2=2,
学考君话您知:S△=×水平宽×铅锤高。
因为点P在二函图像上,所以它的坐标可设为(x,-x2+2x+3),用含x的式子表示铅垂高或水平宽,S△=×水平宽×铅锤高列式即可。
是不是觉得收获满满呢?赶紧拿去刷题吧!